Features

Earlier this year, Professor Eleanor Stride from Oxford University's Institute of Biomedical Engineering won the 2014 IET A F Harvey Engineering Prize.

The £300,000 prize, given by the Institute of Engineering and Technology (IET), recognizes Professor Stride's work using microbubbles for targeted drug delivery, an innovation which aims to avoid the side-effects of current treatment for diseases such as cancer.

Sir John O'Reilly, Chair of the IET's Selection Committee for the Prize, said: 'Professor Stride's research in drug delivery and biomedical ultrasonics is an excellent example of the innovation that can be achieved from the cross-fertilisation of engineering and biomedical sciences.' 

I caught up with Professor Stride to talk to her about her research interests, and where her research is headed in the future.

OxSciBlog: Bubbles have been a common theme in your research career - why are they so interesting?
Eleanor Stride: The bubbles we use in our research are very similar to the soap bubbles you would have blown when you were a small child: a sphere of gas caught in a thin film. We use something a little bit more bio-compatible than washing-up liquid though, and our bubbles are about a 100 times smaller than a human hair. They are fantastic in many, many ways.

I first got interested in their use in a completely different area: I was working as a mechanical engineer during my undergraduate degree, imaging oil pipes to try and increase the yield of oil. In order to figure out what was going on inside these oil pipes, we needed a non-invasive tracking system. Bubbles are great for this, since they produce a strong echo from ultrasound. So we bubbles to track the flow in the oil pipes.

My supervisor then had a completely serendipitous meeting with a radiologist, who turned out to be doing something very similar in the body to track blood flow. We agreed that this was a much more interesting problem, and it also didn’t involve travelling to oil rigs!

So I moved from imaging oil pipes to imaging in the human body. This turned out to be the start of my Ph.D.

One of the very exciting developments in the early 1990's was the realization that the ultrasound could not only be used to track micro-bubbles, but also as a means to deliver drugs. So you have a tiny bubble containing both gas and a drug, that can be used as a drug-delivery vehicle.

OSB: Why are these microbubbles better than traditional methods for getting medications into people?
ES: The conventional way of delivering a drug is to give it as a pill, or inject it into the bloodstream. In either case, the drug eventually ends up in the bloodstream, and the entire body is exposed to it.

This is fine if you’re trying to treat quite a diffuse condition, but for conditions like cancer or stroke, we'd ideally like to target the drug as much as possible to the disease site only. This is because these drugs are very powerful, and can therefore have many side-effects.

What a micro-bubble allows us to do is to put the drug inside the bubble, which means that the drug won't react with any cells in the body until we activate it. So we now have a means of controlling where a drug is released, which means fewer side-effects.

OSB: How do know you when the microbubbles are at their target, and how do you activate them once they are in position?
ES: We use ultrasound for both: since the bubbles produce a strong echo on ultrasound images, we can track their progress.

Secondly, since the bubbles are filled with a gas, they're compressible. Ultrasound is basically a varying pressure wave. This means that when the bubbles are exposed to ultrasound, they alternatively expand and contract. If you turn up the ultrasound power enough, the bubbles will eventually rupture, releasing their contents. So by varying the ultrasound power, we can control when the drug is released.

The other intriguing effect is that this process seems to make cells themselves more permeable: not only are we releasing the drug, but were also helping it get into the body’s cells. We don't completely understand the mechanisms for this increase in permeability. It may be an effect of ultrasound alone, and the bubbles just focus that effect, but it is more likely to be the combination of the ultrasound and the bubble: the motion of the bubble may be setting the liquid around it into motion, and this might be having a shearing effect on the cell-membrane. Or the contact between the moving bubble and the cell membrane might be the crucial mechanism. We're still trying to understand what is going on here.

OSB: Amongst many others awards, you've previously also won the 2010 Venture medal from The Worshipful Company of Armourers and Brasiers, an organization probably less familiar to most readers. What was this prize for?
ES: That was for another project, treating urinary tract infections (UTIs) by improving delivery of antibiotics.

UTIs are a huge problem, especially in the elderly population, where a significant proportion of cases becomes chronic. Oral antibiotics are no longer effective for these patients, so dosages have to be stepped up. The side-effects of the drugs then start to exacerbate the infection itself.

We have been working with our clinical collaborators to develop a way of encapsulating antibiotics so that they are released very slowly over time. This means that a concentrated dose of antibiotics could be delivered slowly and locally to the bladder wall, without exposing the whole body to these high doses.

OSB: What sort of work do you plan to do with the new funding from the IET prize?
ES: One of our big challenges in working with microbubbles is actually making them.

The state-of-the-art is not all that far removed from a cappuccino machine: we bubble a gas and the drug we want to encapsulate into a liquid containing the material that we want the bubbles to be coated with, and we then agitate this mixture using ultrasound to generate a foam (a process known as sonication). We then extract microbubbles from this foam.

We can't control the size of the bubbles or the amount of the drug each bubble contains via this method: it's very quick, but a very crude process.

The grant from the IET prize is to develop a new device that provides the speed and stability offered by commercial industrial processes with the precise control over bubble properties offered by lab based techniques. Making tiny bubbles through this combined ‘microfluidic-sonication’ process will allow much better control of the size and properties of the bubbles we use.

We want to have the best of both worlds!

Professor Stride gave the A F Harvey Prize Lecture on 21 May 2015 at the Royal Society of Medicine in London. 

It is possible to measure oxygen concentrations in sea water in the remote past, a study published this month in Nature Geoscience demonstrates.

These measurements can then be used to infer changes in carbon from biological sources.

This information could potentially be very important for calibrating climate change models, giving an insight into the past that could help predict future climate conditions.

In the study, researchers at Oxford, Cambridge and Hamburg reconstructed oxygen concentrations at the bottom of the ocean from nearly 22,000 years ago. During this time-period (known as the Last Glacial Maximum, the LGM), ice-sheets covered most of North America, northern Europe, and northern Asia. In Britain most of the north (including Yorkshire and the Lake District) and large parts of Wales would have been under an ice sheet.

I asked lead author Dr Babette Hoogakker from Oxford University’s Department of Earth Sciences how the team were able to reconstruct deep ocean conditions from thousands of years ago, and what these results mean for the future.

OxSciBlog: How did you go about measuring deep ocean conditions from such a long time ago, and in such an inaccessible location?
Babette Hoogakker: We did this by looking at the shells of two species of benthic foraminifera (single-cell, deep ocean bottom dwelling animals with a chalky shell) sampled from a deep Atlantic ocean sediment core. These animals are sensitive to physical changes in the environment around them, so their shells can serve as a record of environmental conditions around the animal: they have been used extensively to reconstruct sea water properties.

OSB: What is the link between these fossil animals and oxygen levels?
BH: Oxygen is needed for the breakdown and decay of organic material settles in the sediment at the bottom of the ocean. By measuring the relative levels of different carbon isotopes, we can track the amount of this breakdown. We also already know that the more oxygen there is in the overlying sea water, the more organic material gets broken down.

But as you go deeper into the sediment, more oxygen is used up, until there just isn't enough oxygen for the breakdown of organic material. This is the anoxic boundary.

We could track this boundary by comparing the levels of carbon isotopes in the shells of Cibicidoides wuellerstorfi, which live just on top of ocean floor sediments, versus Globobulimina spp., a related species which lives burrowed down into sediment, at the anoxic boundary.

By comparing carbon isotope levels between these two species, one of which had lived in seawater and one which had lived at the anoxic boundary, we could work out oxygen concentrations at the bottom of the sea.

In doing so, we came up with the first quantitative measurements of deep water oxygen levels in the remote past.

OSB: Were the measurements as you had expected?
BH: From other measurements we knew oxygen concentrations were likely to be lower, but until now we just didn't have any way to quantify by how much!

The solubility of oxygen in seawater increases as temperatures fall. So during the Last Glacial Maximum (LGM), the oceans could well have contained more dissolved oxygen.

Instead, we found that during the LGM, ocean oxygen levels were 20% lower than today.

We know that ocean circulation was very different during the last ice age, so this reduction could be because of slower renewal of deep ocean waters. Another reason for the lower oxygen levels could be that more organic material was being broken down, because more organic material sank to the deep ocean.

OSB: What effects did this increased decay of organic material have?
BH: As organic material breaks down, it releases the carbon it had contained back into the water, where it forms dissolved chemical compounds such as bicarbonate. So the result of this increased decay was that there was more dissolved carbon in the oceans, meaning that the oceans acted as a significant sink for carbon.

From measurements of fossil air trapped in ancient ice cores, we already know that there was a significant decrease in atmospheric carbon dioxide during the LGM. We calculate that 15% of this decrease is due to the process we found: more decayed carbon being locked away in the ocean.

OSB: What implications do these reconstructions of the past have for future climate?
BH: These results provide further information for testing computational models of climate change: they provide quantitative constraints for changes in deep ocean oxygen and organic carbon during times of natural climate change.

More importantly, as the ice-caps melt due to man-made warming, projected changes in ocean currents make it likely that there will be less oxygen in the oceans in the future.

Ocean ‘dead zones’ (such as areas deprived of oxygen) do indeed appear to be expanding as a result of human-induced climate change. Such dead zones affect marine life, and the resulting changes in fisheries and the food chain are likely to have major socio-economic implications.

It was standing room only as Marcus du Sautoy and Ben Okri discussed the relationship between narrative and proof at the Mathematical Institute on Tuesday evening (20 January).

The full video of the event to launch The Oxford Research Centre in the Humanities' (TORCH) 'Humanities and Science programme can be seen here.

The speakers have given Arts Blog permission to publish edited extracts of their talks:

Marcus du Sautoy, Simonyi Professor for the Public Understanding of Science, Oxford University

In Borges's short story The Library of Babel the librarian who narrates the story begins with a description of his place of work:

The universe (which others call the library) is composed of an indefinite and perhaps infinite number of hexagonal galleries...From any of the hexagons one can see, interminably, the upper and lower floors.

As befits a library, this vast beehive of rooms is full of books. The tomes all have the same dimensions. 410 pages, each page with 40 lines and each line consisting of 80 orthographical symbols of which there are 25 in number.

As the librarian explores the contents of his library he finds that most of the books are formless and chaotic in nature but every now and again something interesting appears. He discovers a book with the letters MCV repeated from the first line to the last. In another, the cacophony of letters is interrupted on the penultimate page by the phrase Oh time thy pyramids and then continues its meaningless noise.

The challenge the librarian sets himself is to determine whether the library is in fact infinite or, if not, what shape it has. As the story develops a hypothesis about the library is proposed.

The Library is total ... its shelves register all the possible combinations of the twenty-­‐odd orthographical symbols (a number which, though extremely large is not infinite): in other words, all that it is given to express, in all languages. Everything.

The library contains every book that it is possible to write. When it was proclaimed that the Library contained all books, the first impression was one of extravagant happiness. But this was followed by an excessive depression. Because it was realized that this library that contained everything in fact contained nothing.

So what is in the mathematican’s library? I think many believe that it is aspiring to be a mathematical Library of Babel. That the role of the mathematicians is to is to document all true statements about numbers and geometry. The irrationality of the square root of 2. A list of the finite simple groups. The formula for the volume of a sphere. The identification of the brachistochrone as the curve of fastest descent.

Mathematics though is very different from simply a list of all the true statements we can discover about number. Mathematicians, like Borges, are story tellers. Our characters are numbers and geometries. Our narratives are the proofs we create about these characters.

Let me quote one of my mathematical heroes Henri Poincaré articulating what it means to do mathematics:

To create consists precisely in not making useless combinations. Creation is discernment, choice...The sterile combinations do not even present themselves to the mind of the creator.

Mathematics, just like literature, is about making choices. What then are the criterion for a piece of mathematics making it into the journals that occupy our mathematical library? Why is Fermat’s Last Theorem regarded as one of the great mathematical opus’s of the last century while an equally complicated numerical calculation is regarded as mundane and uninteresting. After all, what is so interesting about knowing that an equation like xn+yn=zn has no whole number solutions when n>2.

What I want to propose is that it is the nature of the proof of this Theorem that elevates this true statement about numbers to the status of something deserving its place in the pantheon of mathematics. And that the quality of a good proof is one that has many things in common with act of great story telling.

My conjecture if I was to put it into a mathematical equation is that
"proof = narrative."

A proof is like the mathematician’s travelogue. A successful proof is like a set of signposts that allow all subsequent mathematicians to make the same journey. Readers of the proof will experience the same exciting realization as its author that this path allows them to reach the distant peak.

Very often a proof will not seek to dot every i and cross every t, just as a story does not present every detail of a character’s life. It is a description of the journey and not necessarily the re-enactment of every step. The arguments that mathematicians provide as proofs are designed to create a rush in the mind of the reader. The mathematician GH Hardy described the arguments we give as 'gas, rhetorical flourishes designed to affect the psychology, pictures on the board in the lecture, devices to stimulate the imagination of pupils'.

What is important for me about a piece of mathematics is not the QED or final result but the journey that I’ve been taken on to get to that point, just as a piece of music is not about the final chord. It is certainly important to know that there are infinitely many primes but the satisfaction comes from understanding why.

The joy of reading and creating mathematics comes from the exciting “aha” moment we experience when all the strands seem to come together to resolve the mathematical mystery. It is like the moment of harmonic resolution in a piece of music or the revelation of who-­‐dunnit in a murder mystery.

The element of surprise is an important quality of exciting mathematics. Here is mathematician Michael Atiyah talking about the qualities of mathematics that he enjoys:

I like to be surprised. The argument thatfollows a standard path, with few new features, is dull and unexciting. I like the unexpected, a new point of view, a link with other areas, a twist in the tail.

When I am creating a new piece of mathematics the choices I will make will be motivated by the desire to take my audience on an interesting mathematical journey full of twists and turns and surprises. I want to tease an audience with the challenge of why two seemingly unconnected mathematical characters should have anything to do with each other. And then as the proof unfolds there is a gradual realization or sudden moment of recognition that these two ideas are actually one and the same character.

The importance of the journey to mathematics can be illustrated by a strange reaction that many mathematicians have when a great mathematical theorem is finally proved. Just as there is a sense of sadness when you come out the other side of a great novel, the closure of a mathematical quest can have its own sense of melancholy.

I think that we’d been so enjoying the journey that Fermat’s equations had taken us on that there was a sense of depression that was mixed with the elation that greeted Andrew Wiles’s solution of this 350 year old enigma. That is why proofs that open up the ground for new stories are valued very highly in mathematics.

Ben Okri, author of Flowers and Shadows, The Famished Road (Booker Prize winner 1991), Songs of Enchantment and Infinite Riches

Narrative is woven into the fabric of consciousness as mathematics is woven into the fabric of the world. If it were possible to imagine a consciousness at the heart of all things in stone, in the air, in trees, in mountains, in stars in atoms, in all things that constitute reality, that consciousness would perceive the world in its smallness, as well as in its largeness, as a grand perpetual narrative.

The motion of things is the story of things; the constant change that Heraclitus saw, the mutations the compositions, visions, collisions, growths, deaths, fissions are all part of the infinite narrative that is reality. It would seem that story is implicated in the world, on the condition that there is a consciousness to perceive it. To that degree narrative is woven into the fabric of the mind. Is there a mathematical basis to narration? Is there a mathematics of narration?

We see from Marcus’s excellent paper that there could be said to be a link between proof and narration, that to prove is to narrate. In literature narrative is a kind of proof. It is more than that of course, but it is always a kind of proof. It is the out figuring of an intuition of tension, of the need for psychic resolution, the need to make visible in order to make understandable.

But narrative as proof takes a more intangible, more aesthetic form. The desire to write a story is not merely to prove the existence of the story in the mind, for often the story does not exist until it is written; it exists in an ideal state, as a throb as Nabakov would call it, an impulse, a pressure on the literary glands, an ache in the soul. But as something cannot come from nothing, the existence of story is proof in a way of a previous intangible condition, a sediment, a concretisation of an opalescent state.

There is one way in which narrative shares a profound similarity to mathematics and this in the unavoidable logic of storytelling. The equation must work. Where the story begins, how it evolves, where it goes, must work, it must add up, it must compute. There is mathematics in narration, in the sense that we know when a story's mathematics does not work. This can happen in a quantum sense at the level of sentences, or in a larger sense in terms of the whole. Narration conforms to an aesthetic mathematics, and the best storytellers therefore are profound and rigorous thinkers. To work out the inner maths of a story or a novel is one of the most difficult things that writers do. For on the rightness of that maths, the unfolding of character within the limitation of plot, rests the immortality or oblivion of the text.

Mathematics is not just what mathematicians do, mathematics – the relation of number – is implicated in the structure of reality, in the number of vibrations that make the atom in the periodicity of elements, and the pulsing of quasars and the calyxes of flowers, in the rhythm of all things. In fact it is the relationship between the rhythmic quality of the world and the rhythmic quality of art that so fascinated Leonardo da Vinci. It would seem that the world, its underlying structure, is governed by known and unknown laws of mathematics. That, as Pythagorus implied, number governs the world, the materiality of the world, the manifestation of things.

It is now axiomatic in practical science that by altering the number of the vibrations of a thing you can alter its nature. I have found this to be true in narration as well. There is a novel of mine called Astonishing the Gods, whose nature was changed by altering its underlying beat, its vibration. I will give you an example. In the early draft it began "invisibility is best". The novel was written in that contracted beat. When I came to write it and to re-write the rewriting I realised that there was something not right about that beat for that novel. In the final version it reads "It is better to be invisible".

A great difference in the unfolding of the text emerged from altering the microbeat of the novel. You could call this re-writing but I believe it is something more. I believe that everything exists by virtue of the law of numbers, its underlying vibration. The elements have their rates of vibration, at atomic and subatomic level all is number, all is vibration, this too at the larger levels. The world is what it is by virtue of this quality. This is beyond the scope of our present conversation, but one can conjecture there might also be a sublime mathematics and that someday could reveal that which we now see as transcendent.

Mathematics is woven into the fabric of the world, narrative into the fabric of consciousness; they are both part of the fact of reality. The world exists by virtue of numbers and the fact that the world exists already implies its narrative quality. The curious thing about both is it they need an intelligent consciousness to perceive their existence.

But there are fundamental differences between proof and narration. One is the universality of language, the transparency of narration. Another is the dual nature of narration that it is both of time and timeless. Another is the mimetic quality of narration, that it mirrors the world, it mirrors modes of consciousness, and in its imaginative dimension it contains matrixes of the future.

One could say that the purity of mathematics makes it more akin to music. Both create realms of their own, crystalline and pure, immaculate fantasies with unalterable laws. Another crucial difference is the fact that great narration has higher immeasurable symmetries. The difference between a well plotted detective novel and Hamlet is infinite resonance. This is not a disquisition on lowbrow and highbrow. A murder mystery of Agatha Christie, for example, is satisfying in tying up all the loose ends, but the resolution of Oedipus Rex gives us unending insight into the complexity of fate, the human condition, and the moral law.

The refractions of Oedipus Rex resonates 2500 years later and the chief reason, I believe, is that it lives, and it partakes of higher truths that we still have not fully grasped. And it compels us to contemplate all the dimensions of what it means to be human. This brings me to the greatest difference between narrative and proof, between mathematics and narration. Narration is, at its highest, about the enigma of being human, of being alive, of consciousness itself, in all of its states, in all its realities, in all its unrealities.

Narration is the highest tool the human mind has devised to investigate the mystery of life and the human condition. It is more than a mirror of the world and ourselves. It is more than an order perceived in the chaos. It is a technology we have dreamt up to help us get from our darkness to our progressive light. I believe that the oldest technology is not the wheel, not the discovery of fire, not even the discovery of language itself. I believe it is storytelling.

We tell stories even without language. We tell stories with our faces, in our gestures, in our eyes. We tell stories on cave walls. I believe the impulse of narration has led us to language and not the other way around. Language amplifies the power and scope of narration. Narration is implied in germination, procreation and cessation. Narration begins before birth and continues after death. Archaeology confirms the latter. Ovid’s Metamorphosis hints at the fact of change which is at the heart of narration.

The big bang was an event of incalculable mathematical magnitude, but it was also a singular narrative event. It could also be called the big beginning. In that moment of astonishing singularity was born the mathematics of all things and the narrative of all things - two children of the same mother-father moment, that brings us all here today.

'Narrative and Proof' was held at the Mathematical Institute on 20 January 2015 at 5pm. Sir Roger Penrose and Professor Laura Marcus also spoke at the event, which was chaired by Professor Elleke Boehmer.

Yesterday was 'Museum Selfie Day', where people across the world were encouraged to take self-portrait photographs of themselves visiting a museum and share it on social media.

Oxford University’s museums were used as the location for dozens of 'selfies'. Arts Blog has picked out some of the best.

Rachel, a trainee on the HLF Skills for the Future Museum Education & Outreach scheme at Oxford University Museums & Collections, used a bushy prop for her selfie with a samurai at the Pitt Rivers Museum. This man is from the peaceful years of the Edo period (1603-1868) in which armour was more decorative than functional so he would probably forgive Rachel for her joke.

Pitt Rivers Museum

Hannah, another trainee on the Skills for the Future scheme, took time out from preparing a tour for Oxford Brookes students to take a selfie in front of a painting of Lewis Evans. Mr Evans, who founded the Museum of the History of Science, is holding one of his sundials, which were ‘his greatest interest’.

A visitor to the Ashmolean Museum mimics the pose of Augustus. Do not be fooled by the clever photo crop - Augustus is pointing, not holding a camera.

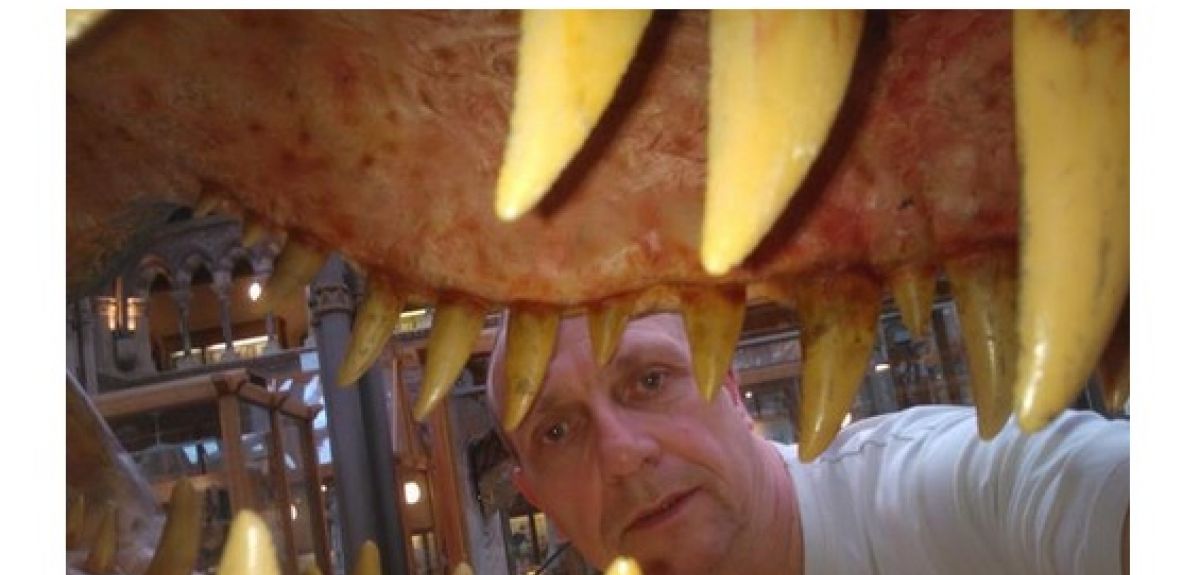
Gary, a cleaner at the Museum of Natural History, snapped himself through the jaws of a dinosaur at the Museum of Natural History. The dinosaur displays in the Museum include four species from Oxfordshire.

Selfies have been criticised as a symptom of a culture of selfishness and celebrity-worship. But we can assure Arts Blog readers that vanity in Oxford is nothing new, as this Muse on the Clarendon Building shows.

Leading figures from humanities and the sciences will discuss the importance of narrative in scientific proofs at Oxford University today.

The event marks the launch of the 'Humanities and Science' series organised by The Oxford Research Centre in the Humanities (TORCH) and will take place at the Mathematical Institute at the University of Oxford.

Mathematician Marcus du Sautoy, Oxford’s Simonyi Professor for the Public Understanding of Science, will give a presentation on role of narrative in mathematics. He will be joined on a panel by author Ben Okri, Oxford mathematician Roger Penrose and Oxford literary scholar Laura Marcus. The event will be streamed live online from 5pm.

Professor du Sautoy will argue: 'Mathematics is more than just true statements about numbers. Why does a proof of Fermat’s Last Theorem get celebrated as one of the great achievements of 20th century mathematics while an equally complicated calculation is regarded as mundane and uninteresting? Why is the proof more important than the result itself? It is not the QED but the pathway to that QED that mathematicians care about. Is the quality of the narrative journey of the proof actually what elevates a sequence of logically connected statements to be celebrated as mathematics? And what qualities does that narrative share with other narrative art forms?'

The discussion will be chaired by Elleke Boehmer, Professor of World Literature at Oxford. She said: 'Literary narrative and mathematical proof, far from being poles apart, in fact fall into intriguingly similar symbolic patterns: stage by stage sequences, tricky reversals, surprising denouements. Indeed, we might go so far as asking ourselves to what extent proofs are in fact narratives of a kind, and narratives a form of proof.'

TORCH's Humanities and Science series will focus on the relationship between the two disciplines, exploring how new answers can be found and new research questions can be set. It will showcase many of the existing research projects in Oxford that already cross the disciplines and provide an incubation space for new collaborative projects.

The dates for future public events as part of the series are on the TORCH website.