Halloween special: zombies vs maths

Zombies reportedly want to eat our brains ("BRAIIINS!") but what if we could use our grey matter to survive a zombie apocalypse?

Thomas Woolley from Oxford University's Mathematical Institute has been figuring out how maths could help us when an epidemic of the undead is unleashed – and in a fun way explore some of the maths behind the study of real life human diseases.

In a chapter in a new book, Mathematical Modelling of Zombies, Thomas and his co-authors report how their models suggest three top tips for avoiding becoming zombie chow:

1. Run! Your first instinct should always to be put as much distance between you and the zombies as possible.

2. Only fight from a position of power. The simulations clearly show that humans can only survive if humans are more deadly that the zombies.

3. Be wary of your fellow humans.

But assuming the shuffling hordes aren't already battering down your front door, I thought I’d take time out from stockpiling cricket bats, shotgun cartridges, and tinned food to quiz Thomas about maths, zombification, and watching your back…

OxSciBlog: How does zombie modelling relate to modelling real diseases?
Thomas Woolley: Mathematics can model the spread of any disease. The critical task in constructing a specific disease model lies in understanding the mechanisms by which the disease is able to spread. Canonically, zombies transmit their disease through biting a victim. Thus, like many real diseases, such as AIDS and Ebola, transmission occurs through contact with infected body fluids. As such, we model a zombie infection using the same techniques and equations that are used to model the aforementioned real diseases.

One of the main differences between zombiism and a real disease is that with a real disease there is usually some hope of a cure, treatment, or recovery. Unfortunately, this does not appear to be the case for zombification. This lack of recovery is one of the primary reasons why it is so hard to stop the apocalypse scenario that appears in numerous zombie films.

OSB: Why, mathematically, is running away from zombies a good strategy?
TW: Our model is based on the idea that zombies move around using a random walk. Explicitly, they are mindless animals that simply lurch from position to the next with no purpose or direction (we apologise for hurting the feelings of any intelligent zombies who are currently reading this). Through this assumption we find that the zombie's motion is described by the diffusion equation.

It is impossible to overstate the importance of the diffusion equation. Whenever movement can be considered random and directionless, the diffusion equation will be found. This means that, by understanding the diffusion equation, we are able to describe a host of different systems such as heat conduction through solids, gases (eg smells) spreading out through a room, proteins moving around the body and molecule transportation in chemical reactions, to name but a few of the great numbers of applications.

Through the use of the diffusion equation we find that the time for a human-zombie interaction is quadratically proportional to the distance separating the humans and zombies, whilst linearly proportional to the zombie diffusion constant, which measures the rate at which the zombies move. Explicitly, this means that if you double the distance between you and a zombie, then the time before your interaction quadruples. However, if you slow the zombies down by a half then the interaction time only doubles. Hence, we see that running away, rather than slowing the zombies down, is the better way of rapidly increasing the time before an interaction.

OSB: What difference does how deadly humans are compared to zombies make?
TW: In our model we suppose that there are three different interactions that can occur:

humans kill zombies at a rate a;
zombies kill humans at a rate b;
humans become zombified at a rate c.

These interactions are illustrated in the figure below. The only way that humans can survive is if we can wipe out the zombie menace. If any remain then they will always represent a potential threat. This means that humans have to kill the zombies at a rate faster than they are created, explicitly we need the rate a to be great than the rate c. Unfortunately, if the zombies are very infectious and very resilient to our attacks then c will be greater than a and we find that an infection wave can take hold in the susceptible population. This results in a scenario where everyone is eventually wiped out.

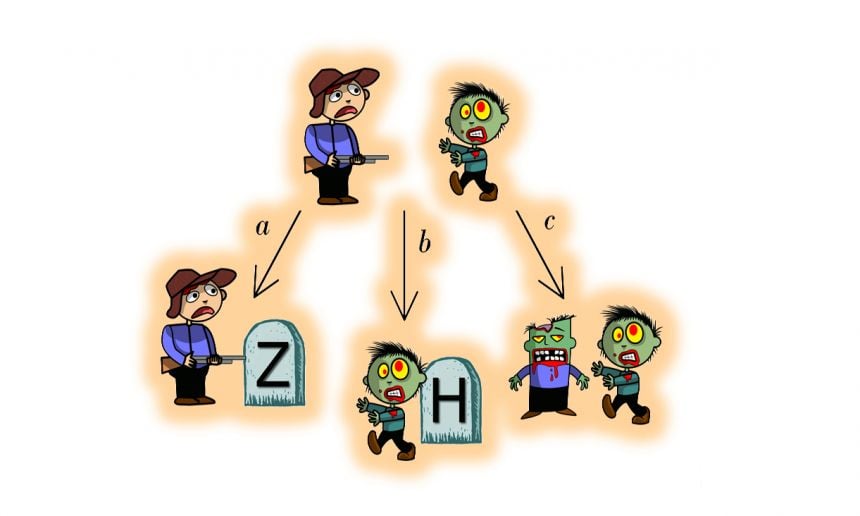Illustration of three possible zombie interactions considered in the model

Photo: Thomas E Woolley, with thanks to Martin Berube who provided the zombie figures.

OSB: Why might maths suggest that you turn on your fellow humans?
TW: An infection wave can only happen if there are susceptible people to be infected. Critically, the speed of the infection wave depends explicitly on the initial number of susceptible people. If you are able to isolate yourself geographically on an island then you should be completely safe (excluding such cases that occur in the film Land of the Dead).

However, suppose you are not lucky enough to live on an island and, instead, you in an office block when the dead begin to rise. Everyone around you is a potential zombie. Thus, be careful to pick your colleagues carefully. If they are all weak then you might want to think about dispatching them.

Alternatively, if you are the weak connection, make sure that someone is not trying to get rid of you. Of course I and the other authors would not recommend such unethical behaviour. The population will have enough trouble trying to survive the hordes of undead, without worrying about an attack from their own kind!