
How to design an icosahedral quasicrystal through directional bonding, by Professor Jonathan Doye
 Prof. Jonathan Doye
Prof. Jonathan DoyeMost people who have done some chemistry will have seen examples of how the directionality of the covalent bonding for a given element can determine the crystal structures they form. For example, the tetrahedral bonding of carbon atoms naturally leads to the crystalline structure of diamond. But to better understand this challenge, we first need to explain what a quasicrystal is.
We should start with a discovery of Sir Roger Penrose, an Oxford mathematician and physicist who won the Nobel Prize for Physics in 2020. In 1974 he showed that one could tile a plane with just two types of tiles, such that the tiling has no repeating pattern but has a kind of 5-fold symmetry that is not possible for crystals. These Penrose tilings, one of which is shown below, are said to have “quasiperiodic order”.
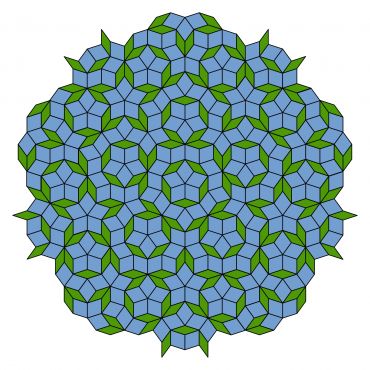 An example of a Penrose tiling
An example of a Penrose tiling
The order of these quasicrystals is revealed by the diffraction patterns that result when electrons or x-rays pass through them. They are labelled as icosahedral, because like the icosahedron that is one of the Platonic solids, there are six axes along which five-fold symmetry is revealed in the diffraction patterns. Like crystals, this underlying symmetry can also be revealed by the shapes into which quasicrystals grow, such as the dodecahedron below. Dan Shechtman’s paradigm-shifting discovery led to him receiving the Nobel Prize in Chemistry in 2011.
 A large quasicrystal with a docahedral shape that is a consequence of its underlying non-crystallographic icosahedral symmetry
A large quasicrystal with a docahedral shape that is a consequence of its underlying non-crystallographic icosahedral symmetryThis discovery led to an intense search for other examples of icosahedral quasicrystals. Many were found, including even natural examples in meteorites, but all were metallic alloys, whereas none have been found in covalent materials where the bonding is directional.
This raises the question of whether, if one is not restricted by the geometry of covalent bonding that is allowed by atoms, it might be possible to design particles that could form icosahedral quasicrystals through directional bonding. In 2014 Eva González Noya, my collaborator at CSIC in Madrid, and myself set ourselves the task of finding computational models that could achieve this.
One of the challenges we faced is that the structure of quasicrystals is more complex to describe than periodic crystals. For example, if one has the diffraction pattern for a crystal, one can work out exactly where all the atoms are in the unit cell. However, for an icosahedral quasicrystal, one instead gets a description of the quasicrystal in terms of a crystal in six dimensions!
Some help came from computational experiments by the group of Sharon Glotzer at the University of Michigan in which icosahedral quasicrystals formed in systems without directional bonding. Although these provided examples where the positions of all the particles were known, they revealed another challenge: although the icosahedral quasicrystals have beautiful long-range order, locally they are quite disordered. For example, if one was to try to have particles that reproduce all the different patterns of local bonding in this example, the number of types of particles needed would be far too large to be practical.
Progress was gradually made, a key insight being that one should not be too fussy about whether a particle is able to form all its possible directional bonds, and in 2018 a first example system consisting of five particle types was found that assembled into an icosahedral quasicrystal in simulations; later, this was simplified to a system of two particle types.
And to show the generality of the design principles, a second quasicrystal-forming system was developed that had a totally different pattern of local directional bonding. Somewhat like the metallic alloy examples, key building blocks are icosahedral clusters (the yellow and cyan rhombic triacontahedra in the image below) which form in a matrix of particles that propagates the global order.
 A close-up of a cut through one of the icoshedral quasicrystals grown in our computational experiments viewed along a five-fold axis of symmetry.
A close-up of a cut through one of the icoshedral quasicrystals grown in our computational experiments viewed along a five-fold axis of symmetry.Of course, an important question is whether these computationally discovered quasicrystals could be realized experimentally. Although it is unlikely that they could be formed by atomic materials, atoms are not the only particles that form crystals. Nanoparticles and colloidal particles can also form crystals; for example, precious opals are crystals of colloidal silica spheres and their iridescence results from the diffraction of light by these crystals.
Recently, crystals made up from building blocks made of DNA have been realized. The beauty of these DNA nanotechnology techniques is that the shape of the DNA particles and the interactions between them can be almost arbitrarily controlled. Computational modelling of such DNA particles suggests that making icosahedral quasicrystals from DNA origami particles could well be feasible.
How to design an icosahedral quasicrystal through directional bonding, Published 18th August 2021, Nature.
 What US intervention could mean for displaced Venezuelans
What US intervention could mean for displaced Venezuelans  10 years on: The Oxford learning centre making an impact
10 years on: The Oxford learning centre making an impact Oxford and The Brilliant Club: inspiring the next generation of scholars
Oxford and The Brilliant Club: inspiring the next generation of scholars New course launched for the next generation of creative translators
New course launched for the next generation of creative translators The art of translation – raising the profile of languages in schools
The art of translation – raising the profile of languages in schools  Tracking resistance: Mapping the spread of drug-resistant malaria
Tracking resistance: Mapping the spread of drug-resistant malaria