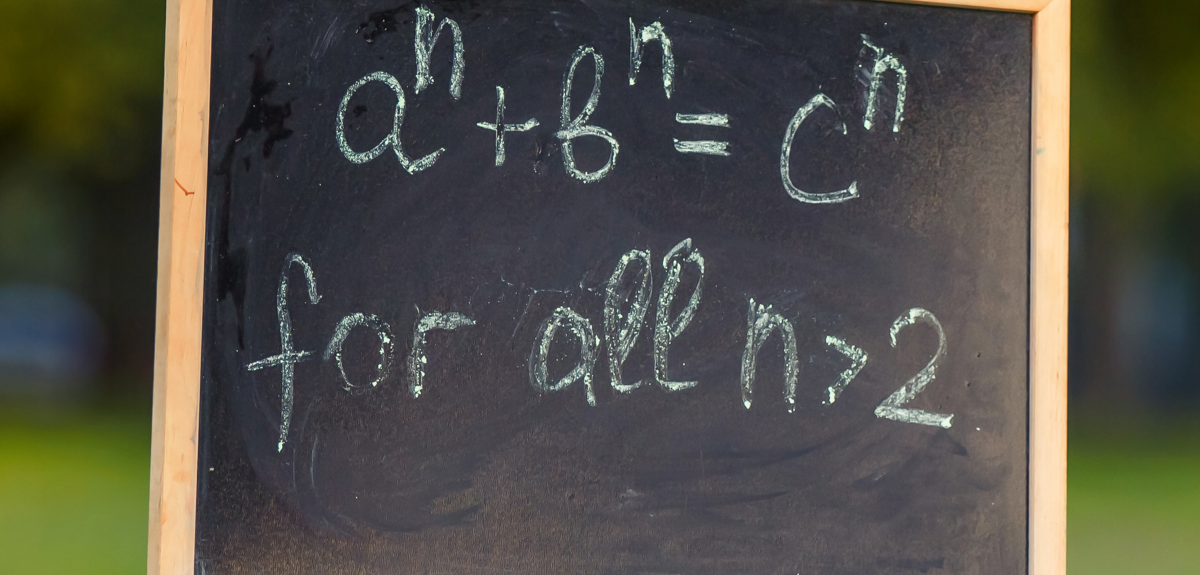
Image credit: Shutterstock
'We all remember where we were when Wiles proved Fermat's Last Theorem'
 Professor Marcus du Sautoy.
Professor Marcus du Sautoy.For the mathematical community it was the announcement in 1993 that Andrew Wiles had finally proved Fermat's Last Theorem. I was in the library at the Hebrew University in Jerusalem on my post-doc year trying to crack the problem I was currently obsessed with when a fellow post-doc excitedly whispered the news in my ear. I can still remember the thrill and excitement of realizing that I was alive at the moment when the most iconic unsolved problem in mathematics had been cracked.
For 350 years we'd been trying to prove Fermat right and now finally we knew that those famous equations xn+yn=zn had no whole number solutions if n was bigger than 2. It is important to recognize that knowing this in itself did not change the landscape of mathematics. What was important was the journey that mathematicians had gone on from that moment, which all began with Fermat's marginal comment about having a proof too big for the margin (surely the biggest tease in mathematical history) to the final QED that Wiles had placed at the end of his proof.
As Wiles always acknowledges, there are many names that carried the baton of the proof from Fermat: Euler, Germain, Legendre, Kummer, Taniyama, Shimura, Weil, Frey, Ribet, Serre and many more. But every mathematician recognized that the seven-year marathon that Wiles ran to complete the proof was an extraordinary feat of mathematics. Before the announcement, no one believed we were anywhere near the finishing line.
But with the sense of excitement though came a slight hint of melancholy. Fermat's Last Theorem had been such a motivating enigma for many of us, there was a sense of sadness that the journey was over, like that moment when you finish a great novel. For the public there was even a belief that Fermat's Last Theorem really was the last theorem, and that we'd 'finished' maths. So it has been important to recognize that although Wiles' work was the completion of one journey, it actually opened up exciting new pathways for new journeys.
I asked Wiles shortly after he published his proof what great unsolved problem he would regard as worthy of replacing Fermat in the public imagination, a problem that would fire up the next Andrew Wiles. He opted for a challenge that has an ancient heritage but a very modern reformulation that is connected with the work he is currently engaged in. The ancient formulation is called the Congruent Number Problem: find a method for determining whether a whole number occurs as the area of a right angled triangle all of whose sides have lengths equal to a fraction.
After centuries of false proofs, Fermat himself proved that the number 1 cannot be the area of such a triangle. Some believe that Fermat thought mistakenly that he could generalize his argument to prove his Last Theorem and that this was what he referred to in the margin.
The Problem of Congruent Numbers is simple to state, and a school child can start playing around with ideas. Yet it relates to one of the deepest questions of arithmetic called the Birch and Swinnerton-Dyer Conjecture, a conjecture that Wiles has been working on for decades and which is one of the millennium problems for which the Clay Institute is offering a million-dollar prize for a solution.
A cryptic marginal tweet by the likes of Andrew Wiles about a proof too big for 140 characters, and perhaps it could find its way into the public imagination as the next great unsolved problem of number theory. Until then, with the award of the Abel Prize for 2016, we continue to celebrate the proof Wiles produced of the greatest enigma of the last three centuries: Fermat's Last Theorem.
Marcus du Sautoy is the Simonyi Professor for the Public Understanding of Science and Professor of Mathematics at the University of Oxford.