Features
 Alessandra Enrico Headrington, COMPAS
Alessandra Enrico Headrington, COMPAS
The United States’ intervention in Venezuela on 3 January 2026 marks a critical moment not only for the country’s political trajectory, but also for the future of one of the largest displaced populations in the world.
The situation before US intervention
The United States’ intervention in Venezuela has ignited questions about its legality under international law and the principles set out in the United Nations Charter. This moment reflects a broader trend in which core legal principles appear increasingly subordinated to power politics. Beyond questions of legality, it also raises deeper uncertainties about Venezuela’s political future and what leadership change might mean for the possibility of return for nearly 8 million Venezuelans displaced since around 2015.
Of the majority of those displaced, around 6.9 million are hosted by countries in Latin America, with Colombia and Peru receiving the largest numbers, followed by Ecuador and Chile, and more recently by Brazil. Since 2015, governments have granted legal stay through the provision of over 5.1 million special, time-limited residence permits. These measures allowed Venezuelans to live and work legally and were initially conceived as rapid and flexible tools to manage large-scale displacement.
This moment reflects a broader trend in which core legal principles appear increasingly subordinated to power politics. Beyond questions of legality, it also raises deeper uncertainties about Venezuela’s political future and what leadership change might mean for the possibility of return for nearly 8 million Venezuelans displaced since around 2015.
However, the limitations of this interim solution have become increasingly visible. Access to temporary permits has grown more restrictive, with the enforcement of tighter eligibility requirements and the reintroduction of border controls. While these schemes have enabled a quick path to legal stay for many Venezuelans, their temporary and conditional nature offer limited certainty about long-term protection or settlement. This policy choice is particularly striking in Latin America, where many states have deliberately incorporated the Cartagena definition into their national frameworks. This regional standard broadens refugee protection to include people fleeing widespread violence, human rights violations and serious public disorder. Under this definition, a significant share of Venezuelans could, in principle, be recognised as refugees, accessing a stronger, rights-based form of protection with greater legal certainty over time in host countries.
Nevertheless, my ongoing doctoral research at the University of Oxford with Venezuelans in Colombia, Peru and Ecuador, points to a clear pattern: many Venezuelans prefer temporary permits, despite their precarious and uncertain nature, over seeking refugee status, which is a protracted and complicated process. Temporary permits are comparatively simple and predictable – even when they involve fees.
But as the political environment shifts, broader questions are likely to arise about the sustainability of temporary permits and about what may come next for the more than 5 million Venezuelans currently living under them.
Will displaced Venezuelans return to Venezuela?
Comparative experience from other displacement contexts, such as Syria, suggests that even significant political or economic shifts in countries of origin do not automatically translate into large-scale return.
For many displaced Venezuelans, recent events symbolise the end of a political era marked with widespread human rights violations, the erosion of the rule of law, and large-scale displacement. These perceptions matter: they shape expectations about the future, influence personal and family decisions, and frame narratives around the possibility of return, even in the absence of immediate material change.
However, while the changing political situation may shape displacement dynamics, return is unlikely to be immediate or uniform.
Comparative experience from other displacement contexts, such as Syria, suggests that even significant political or economic shifts in countries of origin do not automatically translate into large-scale return. International standards make clear that return must be voluntary, safe and dignified, and premised on effective guarantees of physical security, legal protection, access to livelihoods, and institutional stability. In the absence of these conditions, and drawing on comparative experience from other protracted displacement contexts, any return is likely to remain limited and selective rather than widespread.
What may come next for displaced Venezuelans
After more than a decade spent managing Venezuelan arrivals, the question for host countries is no longer how to extend short-term legal stay, but whether this model can meaningfully evolve, or whether a different approach is needed. For most Venezuelans, medium-to long-term stay in host countries across the region therefore continues to be the more realistic horizon. This evolving situation points to three likely scenarios:
- Temporary protection as the dominant response: Temporary permits may continue to define access to legal stay across Latin America, operating largely at governments’ discretion, while refugee protection plays an increasingly limited role. As country-of-origin assessments evolve, this may affect future asylum decisions and, in some cases, the review of existing refugee status under international refugee law.
- Tighter access to legal stay and rising irregularity: Temporary permit schemes could be adjusted, affecting eligibility, duration, and in some cases their continuation. Given their discretionary nature, such shifts could increase legal uncertainty and, over time, push more Venezuelans into irregular status and onward movement.
- Selective return alongside sustained mobility: Voluntary return is likely to remain limited rather than widespread, shaped by continued uncertainty in Venezuela and occurring alongside ongoing mobility, including new departures by groups that had previously stayed in the country, some of whom supported Nicolás Maduro.
The bigger picture
The future of protection for Venezuelans will be shaped both by events in Venezuela and by political and electoral shifts in host countries. Electoral cycles and shifting domestic agendas in countries such as Ecuador, Chile and Peru are likely to influence whether existing legal protections are maintained, progressively narrowed, or increasingly reoriented towards return-focused approaches.
The future of protection for Venezuelans will be shaped both by events in Venezuela and by political and electoral shifts in host countries. Electoral cycles and shifting domestic agendas in countries such as Ecuador, Chile and Peru are likely to influence whether existing legal protections are maintained, progressively narrowed, or increasingly reoriented towards return-focused approaches.
Beyond Venezuela, these dynamics carry broader significance. The Latin American response, marked by the large-scale use of temporary permits and a more limited reliance on refugee protection, offers a revealing case of how states manage protracted displacement with precarious tools and under political uncertainty.
What happens next will affect not only the future of Venezuelans, but also how large-scale displacement is managed in other regional and global contexts, with consequences for society as a whole.
Ian Walmsley, a Professor of Quantum Science and Engineering and an internationally recognised expert in quantum photonics, has returned to Oxford from Imperial College London, where he served as Provost for the past seven years. He was previously Hooke Professor of Experimental Physics and Pro-Vice-Chancellor for Research and Innovation at Oxford. His career has seen him lead the UK’s first Quantum Technology Hub, co-found a quantum computing spinout, and serve on the UK Government’s National Quantum Strategic Advisory Board.
In October this year, he took up the position of Director of the Oxford Quantum Institute (OQI). Here, he reflects on Oxford’s strengths in quantum, the role that the OQI will play to accelerate impact, and how the UK as a whole can remain competitive in the quantum arena.
Your career has ranged across both fundamental and applied quantum science. What first drew you in?
There is a huge opportunity for quantum here in Oxford and a will to succeed. I look forward to getting the Institute underway and collaborating with brilliant colleagues working at the cutting edge of quantum.
My route into quantum was through optical science and engineering - using light as an exquisite sensor to probe systems, to link systems for secure communications, and increasingly to process information in photonic quantum computers. Light is special: it is the one physical medium we can control with extraordinary precision in which quantum effects remain accessible at room temperature. That makes it both a powerful scientific tool and practical technology, with a unique ability to bridge disciplines from astronomy to biomedicine.
I’ve had the good fortune to work with brilliant colleagues across many domains of optics and photonics, but particularly at the conjunction of ultrafast and quantum optics. This combines producing very, very short light pulses with the science of how light behaves according to the rules of quantum physics. One of my earliest directions was to use the brevity of ultrashort light pulses to map the quantum motion of vibrations in molecules, and later to make two diamonds sitting in the lab become “entangled” – meaning their properties became linked in a way that goes far beyond anything possible in everyday, classical physics.
Part of this effort required developing new tools to measure and fully characterise these very brief events, and that led to a commercial device that was used to ensure this category of lasers were performing as you wanted. More recently we’ve used this domain to generate the purest single photons yet made, and enabled quantum photonic platforms for information processing – elementary quantum computers, in fact, though far from a scalable machine.
How has the field of quantum computing changed over your career?
If we can harness the power of superposition (where units of information can exist in indeterminate states), this would unlock computational power far beyond that of classical computers.
Quantum science has been around for over 100 years, but the last two decades have been truly transformative. The key tipping point was the realisation that applying quantum principles to the transfer of information could be a reality and not just a theoretical possibility – unleashing the current intense development effort across engineering and physics. We can now conceive how quantum principles could be used in the future to perform useful work and solve problems.
If we can harness the power of superposition (where units of information can exist in indeterminate states), this would unlock computational power far beyond that of classical computers. As Bill Phillips (1997 Physics Nobel Prize winner) said: ‘A quantum computer is more different from today's digital computers than those computers are from the abacus.’
What is the aim of the Oxford Quantum Institute?
Our aim is to ensure that Oxford fulfils its potential as one of the world’s pre-eminent institutions for researching both fundamental quantum technologies and their impacts on society. Oxford already has exceptional quantum capabilities distributed across many departments; OQI adds value by joining these up. By coming together, we can develop shared concepts and language across disciplines to identify the really big questions and new ways to answer them.
The Institute will have a dedicated space in the Townsend Building to act as a common meeting point for both our diverse research community and external luminaries – from those working in technology governance at Oxford’s Blavatnik School of Government to biochemistry researchers using quantum to study the structure of enzymes.
No known physics forbids fault-tolerant quantum computers, but the technical challenges are formidable.
OQI will also serve as a ‘shop window’ of Oxford’s quantum capabilities to the wider world, providing a portal of access for external institutions to look through to see how they might access these strengths. The exchange of ideas is critical to drive forward research, and OQI will actively work to create opportunities for cross-disciplinary collaborations. A central aim is to create joint research partnerships that allow academics to move seamlessly between universities, research centres, and industry, gaining broad insights that enrich their work.
In short, the goal for the OQI is to set the agenda for the next 100 years of quantum science.
Where does Oxford stand in quantum right now?
Oxford has one of the deepest and broadest concentrations of quantum expertise anywhere, from thinking about the philosophical foundations of the theory to developing the technology for quantum computers and spinning out companies that are already commercially applying quantum principles. The University has played a leading role in the first three generations of the UK’s Quantum Hubs network and has had a large influence on the national agenda. For instance, Oxford is a key partner in the UK's first Quantum Biomedical Sensing Research Hub, launched last year, which is exploring how quantum technologies could transform early disease diagnosis.
At the same time, Oxford is really pushing at the frontiers of fundamental science. For instance, the QUEST-DMC experiment, in which Oxford is a key partner, is using the quantum properties of superfluids as a super-sensitive detector for dark matter. And the AION consortium is using atom interferometry with a similar aim. This is led by Imperial and Oxford, with the next generation large-scale interferometer hopefully to be built here.
It’s this combined breadth and depth that makes Oxford such a stimulating place to be in quantum.
 Quantum research at Oxford University. Credit: John Cairns.
Quantum research at Oxford University. Credit: John Cairns.How long will it be before we have a fully working quantum computer?
How long is a piece of string? The underlying technology for quantum computing has developed rapidly over recent years, and quantum concepts will soon start to impact our everyday lives, for instance room-temperature MRI sensors for brain imaging and ultra-secure communications over a quantum network. No known physics forbids fault-tolerant quantum computers, but the technical challenges are formidable. Until these are addressed, it is still a case of if not when we get to functional fault-tolerant quantum computers capable of realising the full promise of the technology. I am sanguine that we will eventually get there, but that we’ll probably need a few more creative ideas to do so.
Nevertheless, with so much resource being applied to this goal, we can be confident that the journey will result in ‘spin off’ benefits along the way. We can expect hybrid quantum–classical co-processors that can slot into data centres, boosting certain AI and optimisation tasks, sometimes with lower energy or higher accuracy. Another likely application is navigation with quantum accelerometers and gyroscopes that can work in GPS-denied environments. Sensitive quantum probes of sub-surface structures and long-distance quantum key networks are also in commercial prototype stages.
Tell me about your quantum spinout, ORCA computing.
The exchange of ideas is critical to drive forward research, and OQI will actively work to create opportunities for cross-disciplinary collaborations across academia and industry.
I co-founded ORCA Computing in 2019 as a spinout from the first Quantum Computing Hub, which was based here at Oxford. My co-founders were Professor Josh Nunn at the University of Bath, one of my former DPhil students and research colleague, and Dr Richard Murray, from Teledyne, who we met through the first Quantum Hub when he was at Innovate UK - another example of how initiatives that bring academia and industry together can bear unexpected fruit.
Our aim was to apply what we had learned from more than a decade of research at Oxford toward building a flexible quantum computer powered by photonics. The machines we produce store and process information using individual particles of light (photons) travelling through standard optical fibre, rather than electricity. These can plug directly into existing data centre infrastructure to enable organisations to try real-world tasks – such as optimising complex networks or experimenting with AI/machine learning workflows- by running quantum and classical computing side-by-side in a hybrid manner.
We now supply photonic computers for machine learning to a range of international customers including the UK Ministry of Defence, the UK’s National Quantum Computing Centre (UK), and Montana State University (US).
Oxford’s spinout track record in quantum is strong, but what is the outlook for quantum commercialisation in the UK?
The UK is well positioned to develop commercial quantum applications. The UK National Quantum Technologies Programme, which has been in place for 10 years now, has really been a spur to bring together the great scientific ideas based in universities and real-world, user knowledge within industry. The intersection of these has already launched a wide range of quantum spinouts and Oxford has been particularly prolific.
Oxford has one of the deepest and broadest concentrations of quantum expertise anywhere, from philosophical foundations to developing technology and spinning out companies.
However, two things are crucial to ensure that the UK can capitalise on this. First, investing in the skills base. Universities play a vital role in developing highly talented people, but our efforts are compromised if the UK is not seen as open and attractive on the global stage. We need to actively engage with policy makers to ensure that immigration policies and visas, for instance, are aligned with national quantum goals.
The second issue is finance. In the UK, there is a definite funding gap between the stages of launching a seed company and developing the technology to the point of market-readiness. Here in Oxford, we can benefit from investment from Oxford Science Enterprises, but the UK Government needs to think hard on how to attract more venture capital money into the UK quantum ecosystem as a whole.
Do you have a favourite example of a quantum spinout launched at Oxford?
Of course, I’d be bound to say ORCA Computing! But there are many successful companies to choose from. The recent sale of Oxford Ionics based on their trapped-ion gate technology was clearly an outstanding success, and a global endorsement of Oxford’s capacity for creating world-leading tech companies. I’m generally quite fond of all those quantum computing businesses that emerged from the first two Hubs: Oxford Quantum Circuits, Quantum Motion, and Universal Quantum prominent among them.
You can find our news items on quantum-related research at Oxford University here.
For more information about this story or republishing this content, please contact [email protected]
In 2014, IntoUniversity – a national charity that provides local learning centres to break cycles of disadvantage – opened the Oxford South East learning centre in Blackbird Leys in collaboration with the University of Oxford and Christ Church, Oxford.
 Dr Rachel Carr, Chief Executive and founder of IntoUniversity, at the 10-year anniversary event.
Dr Rachel Carr, Chief Executive and founder of IntoUniversity, at the 10-year anniversary event.Set up to support young people reach their potential, over the past decade the centre has supported more than 5,000 local students from the ages of 7 to 18 through school and centre-based educational workshops, homework sessions, mentoring and holiday activities.
Ten years after it first opened its doors, IntoUniversity staff, volunteers, students, teachers and parents share what the centre means to them.
Benjamin Ashton, Centre Manager
Benjamin joined the centre staff in February 2023 as an after-school education worker and earlier this year took on the job of Centre Manager. ‘During the school day we workshop with partner primary and secondary schools – either at the centre or in school. After school, we are back in the centre and students come to us.’
 IntoUniversity students successfully complete a group mentoring programme.
IntoUniversity students successfully complete a group mentoring programme.
Benjamin and his team continue to provide academic support to secondary students but are also helping them to focus on the options available to them when they leave school. ‘Our job isn’t to push our students down any particular path but to present them with all the options. Our main message is: ‘Pursue your interests and your passions’.’
He is clear about the importance of having a physical space for the centre, that is separate from school but rooted in the local community. ‘Community spaces for young people are disappearing. We may have an academic focus, but we can still be that community space,’ Benjamin says. ‘And Blackbird Leys is an incredibly strong community. It’s vibrant, multi-cultural and peaceful. I feel lucky to be part of it.’
Beatrice, Year 12 student
Beatrice, aged 16, has been coming to the centre once a week for four years for help with revision and to complete school assignments. ‘The staff are kind and welcoming, and full of knowledge when I don't know what to do.
 Members of the IntoUniversity team with students at the Oxford South East learning centre.
Members of the IntoUniversity team with students at the Oxford South East learning centre.
‘I am quite an ambitious person but I would say that they push my ambition beyond its limits as they provide me with more information. I also like the events that are organised [in the school holidays] as they are quite fun!’
‘My advice to other young people thinking about attending the centre would be one hundred per cent come here – you won’t regret it’.
Ozioma, Year 12 student
Ozioma found out about IntoUniversity from a friend who came to the centre. Now in Year 12, she has been attending every week since Year 4. She uses her time at the centre to finish off her homework and do some revision. But it feels very different from school, Ozioma says.
‘I like how I get to see and talk to my friends and I like talking to the people who work at IntoUniversity,’ she says. ‘I get to meet new people here and have experiences about university and education that I might not get at school.’
‘Being part of IntoUniversity has made me care more about my education and made me want to go to university. Also, staff can always help with a question that I’m stuck on!’
Caroline Martin, Centre volunteer
‘There is such a positive vibe here,’ says Caroline Martin, who has been volunteering at the centre for the past four years. ‘If I turn up feeling a bit tired, the energy of the staff and children lifts my spirits.’
 Year 6 students enjoying a workshop at the Natural History Museum in Oxford.
Year 6 students enjoying a workshop at the Natural History Museum in Oxford.
‘We follow a different topic each term; this term it’s Computer Science. But really, we are helping the children with their Maths and English. I usually sit with the kids who need extra help.’
Some children just find school overwhelming, Caroline says. ‘The education centre is not school. But it is somewhere people who might be struggling at school can get a little extra help. For many of them it also opens their horizons and that’s a great aim.’
Omotayo, Parent
Omotayo understands the opportunities education offers – and she believes the support of the centre staff in Blackbird Leys is enabling her children to take up opportunities that weren’t available to her.
All three of her children have benefited from the centre; her daughter and younger son still attend regularly.
‘It opened my eyes. If your kids are struggling, there is a place for them to go,’ she says. ‘IntoUniversity has helped my children with all aspects of life. It is teaching them team work and leadership skills. It has helped them focus and boosted their self-confidence.’
‘My youngest child is 10 and he went on an IntoUniversity trip to Southampton University during the summer. Now he wants to go to university too.’
Omotayo’s older son has secured a full scholarship to Marlborough College through IntoUniversity. It is an amazing opportunity for him, Omotayo recognises, and one he wants to share, thanks to the care and support he received from staff and volunteers at IntoUniversity in Blackbird Leys.
‘My children are ready to give back. My son knows he is on a bursary and he knows that he also wants to raise opportunities for others.’
Sarah Bennett, Primary school teacher
 Centre leader Benjamin Ashton with students on a trip to Science Oxford in Headington.
Centre leader Benjamin Ashton with students on a trip to Science Oxford in Headington.
Sarah worked at the centre for three years before completing her teacher training qualifications, and now works as a Year 4 class teacher in one of the centre’s partner schools, Church Cowley St James.
‘From a teacher’s perspective, it’s great that IntoUniversity introduces our pupils to the idea of university as one of the many options open to them after school,’ Sarah says.
‘Our cost-of-living crisis means many families don’t often have these conversations with their children. But IntoUniversity feeds their curiosity early and staff explain briefly how the funding works so that it doesn’t seem too scary, and it opens parents’ eyes to the possibilities for their children.’
Find out more about IntoUniversity here.
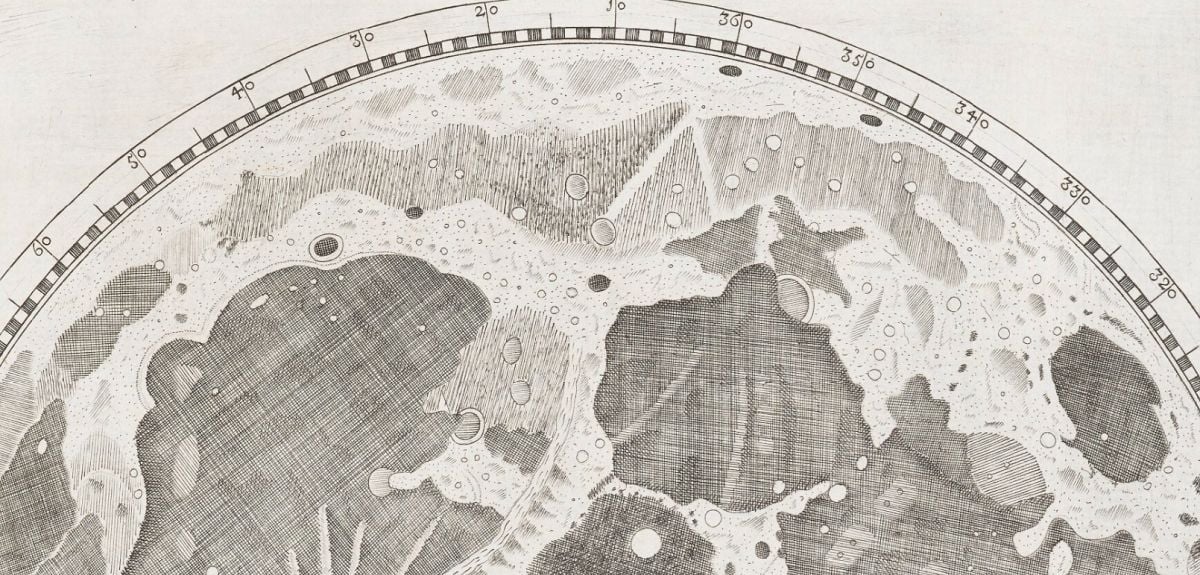
In 1647, a self-taught astronomer and brewer from Gdańsk changed the way humanity saw the Moon by creating the first detailed map of the lunar surface. Now, nearly four centuries later, the Bodleian Libraries have brought Johannes Hevelius’s Selenographia, sive Lunae descriptio ('Selenography, or a Description of the Moon') into the digital age – allowing anyone, anywhere, to explore the world’s very first lunar atlas.
 Portrait of Johannes Hevelius. Date: 1646 – 1649. Credit: Rijksmuseum.
Portrait of Johannes Hevelius. Date: 1646 – 1649. Credit: Rijksmuseum.Selenographia was pioneering in its accuracy, showing that Moon’s surface was far from a blank canvas, but a mosaic of craters, valleys, and mountains. The complete atlas is made up of 111 plates and engravings, showing the Moon in every phase, besides a composite map depicting all of the Moon’s features as if lit from the same direction, which became the model for later lunar maps.
This remarkable artefact is of high interest to astronomers, lunar enthusiasts, and historians of science worldwide. Up to now, those wishing to view it would have to come to the Bodleian in person and arrange for the item to be brought out specially. But now a fully-digitised, open-access version is available through Digital Bodleian, the Library’s showcase platform for digitised collections, for anyone to admire, anytime – even from the comfort of their own home.
Judith Siefring, Head of Digital Collections Discovery at the Bodleian, says: ‘The Bodleian is committed to democratising access to its really amazing collections, and digitising as many manuscripts, archives, and rare books as possible forms a large part of that. Around 75% of those who use Digital Bodleian are based outside the UK, demonstrating that we are serving an international audience.’
A remarkable object from a remarkable man
 A page from Selenographia: sive, Lunæ descriptio. From Bodleian Library Arch. H c.12.
A page from Selenographia: sive, Lunæ descriptio. From Bodleian Library Arch. H c.12. Producing a lunar atlas was one of Hevelius’s first major endeavours, the other being a catalogue of 1564 stars. Over five years, he meticulously drew the Moon each night from observations by eye and through his telescopes, then engraved his observations in copper the following morning.
‘Considering the equipment he was using, the level of detail of the map is mind-boggling,’ adds Malgorzata. ‘Rudimentary maps of the Moon already existed, but none as detailed as this, and none in the form of an atlas. Hevelius took it upon himself to name various aspects of the terrain, indicating that he discovered many details that were not known about previously.’
Many of the names Hevelius gave to lunar characteristics are still used now (such as ‘Alps’ for lunar mountains), and a large crater on the edge of the Ocean of Storms also bears his name today. When the volume was published in 1647, it brought Hevelius fame and prestige as an astronomer, but perhaps the greatest testament to Selenographia is that it stood as the ultimate lunar reference manual for over a hundred years.
Digitising a treasure
 Photographer Ellie Harris in the Bodleian Imaging Studio.
Photographer Ellie Harris in the Bodleian Imaging Studio.The project to digitise Selenographia took shape after the presentation copy was displayed for a group of visiting directors of Polish museums and art galleries. Through collaborations between the Bodleian, the Polish Ball, and the Centre for Democracy and Peace Building, a private donor came forward to fund the digitisation. Malgorzata recalls: ‘Mr Karol Sieniuc was so impressed by the Bodleian’s collections and how it strives to make them available to everyone, that he did not need much persuasion to sponsor the digitisation of a Polish treasure that is Selenographia.’
Selenographia was digitised in the Bodleian Libraries’ dedicated studio, one of the country’s leading imaging facilities. This is equipped with high-resolution cameras and bays tailored to digitise different types of material, from papyrus and maps, to manuscripts and rare books. Over the course of a week, the atlas was captured in just under 800 images at 600-dpi resolution, each checked and aligned using specialist software, then linked to bibliographic data before publication online. The resulting digital version allows users to leaf through Selenographia virtually and zoom in to explore even the finest engraved details, revealing the Moon as Hevelius first saw it nearly four centuries ago.
Connecting communities
 A page from Selenographia: sive, Lunæ descriptio. From Bodleian Library Arch. H c.12.
A page from Selenographia: sive, Lunæ descriptio. From Bodleian Library Arch. H c.12. ‘Digitising collections fulfils many key purposes,’ says Judith. A major one is preservation, of course. Interestingly, much of Hevelius’s observatory, instruments, and books were destroyed by a fire in 1679, and the original copper plate used to print Selenographia was sold after his death and turned into a teapot. ‘Another key purpose is engaging diverse audiences with our collections in new ways, and opening up the knowledge they contain to the world,’ adds Judith.
Digital Bodleian has already made over 1.3 million images of rare manuscripts, maps, and printed works freely available online. Previous major initiatives have included partnerships with the Vatican Library (Greek and Hebrew manuscripts and early printing) and with the Herzog August Bibliothek (medieval Manuscripts from German-speaking Lands), both generously funded by the Polonsky Foundation. Other projects have included Literary Manuscripts (funded by the Tolkien Trust) and Education & Activism: Women at Oxford 1878-1920, a collaboration with several Oxford colleges.
You can find the digital version of Selenographia here.
From inspiring science days for local schools to educational festivals for young people, targeted outreach programmes, the launch of a new online academic enrichment platform, and support for UK-wide access initiatives; across the collegiate University, Oxford is finding new and innovative ways to engage with talented students across the UK from all backgrounds.
Oxford colleges have worked with The Brilliant Club – a UK-wide charity that aims to improve opportunities for students from less advantaged backgrounds to access higher education – for a number of years, hosting ‘graduation’ ceremonies for hundreds of young students completing the Scholars Programme.
 Students visit Oxford colleges and learn more about university life. (c) The Brilliant Club
Students visit Oxford colleges and learn more about university life. (c) The Brilliant ClubIn 2024/25, twelve of Oxford’s colleges formally joined The Brilliant Club’s Scholars Programme, which connects state school pupils, aged 8 to 18, with PhD students who share their subject knowledge and passion for learning.
The scheme enables participants to experience university-style learning through seven in-school tutorials delivered to a small group of pupils by trained PhD tutors, usually based on their own research. The charity has built a community of over 1,200 tutors made up of current PhD students, early career researchers and PhD graduates.
The Scholars Programme introduces pupils to the world of academic research and is designed to help them build confidence, curiosity and a sense of belonging in higher education. It includes a challenging final assignment and for many the experience culminates in their own graduation celebration at one of the University’s colleges.
In 2024/25 more than 1,700 school pupils from Oxfordshire, Buckinghamshire, Bristol and London either worked with an Oxford researcher or attended a graduation event at an Oxford college.
 Dr Matthew Williams work with school groups in his role as Access Fellow at Jesus College
Dr Matthew Williams work with school groups in his role as Access Fellow at Jesus College
The scheme, Dr Williams says, is also a valuable experience for Oxford’s PhD students who receive expert training to develop and hone their pedagogical skills, gain sustained teaching experience, develop research communication skills, and have an opportunity to communicate their research to a non-specialist audience.
Five Oxford PhD students took part in the programme in 2024-25, with specialisms ranging from genetics to archaeology and courses covering subjects as diverse as the healthy heart, the evolution of biodiversity, and neuroscience and AI. ‘Increasingly, PhD students are encouraged to think about public engagement and impact, and this helps them develop key communication skills — being able to explain complex ideas to a 15-year-old is a great test of understanding.’
Abby Williams, a PhD student in the Department of Biology, said, ‘During one of my first lessons we were looking at the animal evolutionary tree, and one of my students had a ‘lightbulb moment’ – we were discussing how humans are more closely related to starfish than insects, and the student said, ‘Miss, that’s really cool!’. That moment felt like a massive teaching win for me, and I hope that the student felt inspired to learn more about the natural world.’
 Students visited Oriel College and graduated from the programme with a formal ceremony. (c) The Brilliant Club
Students visited Oriel College and graduated from the programme with a formal ceremony. (c) The Brilliant ClubDr Williams says the partnership demonstrates how collaboration can deliver genuine impact; ‘Partnering with The Brilliant Club allows Oxford to make a tangible difference in the lives of young people while giving our own researchers meaningful opportunities to share their work. Through initiatives like this, Oxford continues to work with schools, colleges and charities across the UK to inspire the next generation of students to consider Oxford as a place for them.’
Find out more about Oxford University's access programmes - Oxford Access | University of Oxford.
- 1 of 252
- next ›




 What US intervention could mean for displaced Venezuelans
What US intervention could mean for displaced Venezuelans  10 years on: The Oxford learning centre making an impact
10 years on: The Oxford learning centre making an impact Oxford and The Brilliant Club: inspiring the next generation of scholars
Oxford and The Brilliant Club: inspiring the next generation of scholars New course launched for the next generation of creative translators
New course launched for the next generation of creative translators The art of translation – raising the profile of languages in schools
The art of translation – raising the profile of languages in schools  Tracking resistance: Mapping the spread of drug-resistant malaria
Tracking resistance: Mapping the spread of drug-resistant malaria